My First Monoid

My introduction to functional programming was reminiscent of taking a test I hadn’t studied for; enough jargon to construct a fantasy language from and a sinking in the pit of my stomach that told me I was out of my depth. My intitial reaction was a cutting dismissal. There were omens of academia. There was a deluge of tweets from evangelists on the interwebs with words like F-Algebra, Functor and Category Theory. I half-expected to wake up with a copy of The Watchtower on my doorstep. So with my self-esteem at stake I fully intended to shelve the idea away as belonging to robed logicians locked away in research towers. That is until I ran across the concept of a monoid.

The word itself had a metallic taste. Monoid. What the hell was a monoid? I was pretty sure there were some people in the Bible Belt claiming to have been abducted by one. In a sea of terms that could have been Harry Potter spells, this one caught my interest.

Spoiler Alert: It turned out to be a rather simple concept. However, it suffered the same fate as other simple ideas - it had a scary name. The idea seemed to be more an exercise in cleverness. Hearing the twittersphere extol the virtues of monoids, you would think them a panacea for all programming ills. How would monoids help with querysets in Django or make it easier to mock an external dependency in a test? I was asking the wrong questions. I wouldn’t have questioned the utility of plumbing by asking how it could help my backhand in table tennis.

Just get to the point…

• 1 + 0 = ?
• 2 * 1 = ?
• True AND True = ?
• False OR False = ?

Did you notice a pattern?

Let’s look at the first question.

1 + 0 = 1

When we add 1 to 0, we get 1 back. We say that 1 was unaffected by the operation.

This would be the same for any number we add to zero. We’ll always get the same number back guaranteed.

What about the other questions?

• 2 * 1 = 2
• True AND True = True
• False OR False = False

In fact, every question above gives a glimpse into the nature of monoids.

Every example above has some collection or set of objects (e.g., numbers and booleans) a binary operator (this just means it works on two values at once) and a special element of that set that acts just like zero does in addition, or one in multiplication. This element is what’s known as the identity element. It gives you back whatever you gave it.

Now that we have the working parts, we can tease out a definition. A monoid is the combination of a collection of objects, a binary operator and an identity element. If you are missing one of those, you are no longer dealing with a monoid. Monoids also have some properties that afford the wielder a level of mathematical certainty unmatched by any shoddy adhoc abstraction.

• booleans + conjunction + true == monoid
• booleans + disjunction + false == monoid
• numbers + addition + 0 == monoid
• numbers + multiplication + 1 == monoid
• arrays + concatenation + [] == monoid

There are all sorts of them in the wild and when you find them, you know them. You’ve seen their downstairs mixup.

Practical Monoids

Even after this initial aha moment I still felt bereft of any great revelation. Where was the utility in this? It seemed little more than a novel bit of math trivia, something you may see nestled away in one of the blue squares on Jeopardy.

Let’s look at a relevant, albeit naive, programming problem. How would we sum up a list of numbers? Well there are multiple ways to skin a catamorphism.

code samples were made simple by using Carbon

In the example above, we sum (addition as the binary operator) the list of numbers (set of objects) and starting with 0 (the identity element). Since we know that zero added to any number equals that number, we can use it as the beginning operation.

Understanding monoids made the reduce function click for me. Before that I had avoided it like a conversation about religion at a family reunion.

We could do this for any other monoid!

Notice even strings under concatenation (addition) form a monoid with an empty string as the identity element!

Now here’s the icing on top.

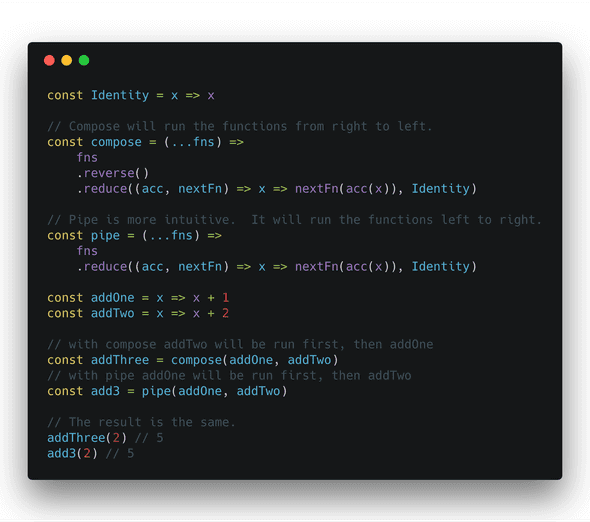
Functions themselves along with an operator called composition and a very special function called the identity function (guess what that does!) form a monoid!

The compose function in the example starts with a list of functions and reverses them (compose will run the functions in the list from right to left, pipe will run the functions from left to right). Since we know that the identity function just gives you back whatever you give it, it is a no-op which means we can use it as a starting point in the same way we’ve done in the examples above. In this specific case, the order of the functions doesn’t matter since addition is commutative.

Composition is really a topic unto itself and admittedly requires a dedicated post. We’ll explore that at a later time.

Just the beginning

There are myriad gems to be discovered in functional programming. Hopefully I’ve imparted some intuition and piqued your interest. Onward!

Hand selected musings by Thomas Manley. You may know him as that guy who sneezed once. Check out all 5 of his tweets.